well, what shape, then?

So what is the correct, optimal theoretical shape for this item, then?  I don't know if there's a mathematical name for it or not, probably, but it's a "cone-oid" with a non-uniform rate of change of radius.  Additionally, the centers of the circles are not co-linear: if they were, this would lead to "Christmas-ornament" shapes or "onion" and "pear" kinds of shapes.  Here, the co-linear portion is basically one edge of the "cone-oid".  More precisely, the paths of the four strings, by definition, are co-linear; the radius at each point is simply the radius of the circle which touches all four strings (there will always be exactly one such circle).  The center of each circle wanders up and down in accordance with the radius, which itself changes in a smooth but non-linear way; but the circle centers are always on the centerline, left-to-right (assuming for now the bass is lying on its back), because the string band layout pattern is symmetrical left-to-right.

Overall, this shape is a little bit "concave": it curves "inward" in the longitudinal axis, where the cone is a straight line.  (Which is part of why I've come to suspect that "real" builders may start with a cone, and then carve out a curved additional volume, to produce this same shape or something close to it, based on experience and "feel" more than mathematics.)

So I don't know a name for this shape, and I don't have an equation for it (yet), and I don't remember it being covered in my Calculus books (unfortunately, since I still have them).  Just to explore and get a feel for how the radius varies, I have been writing some C code...

The idea is to automate the formula for finding the equation of the circle which passes through a given set of three points (any three of the four points can be used, representing the positions of the four strings at a given distance along the fingerboard length).  Thus, we'll know the radius and position of the center, for each location along the fingerboard.  We know these values won't change in a simple linear way, the functions will be some kind of subtle curves.  A proper mathematical analysis would have to include finding the equations of these curves; then the problem would truly be fully subdued.  However, I think that if the curves are not "obviously" some kind of simple shapes like quadratics or exponentials, then it may be sufficient to simply produce a large number of numerical values, without knowing the actual equations.  This kind of data could be used, either with a CNC approach of some kind, or with by-hand construction of jigs and templates.

There are a lot of pages on the Net which touch upon the problem of finding a circle which passes through three given points; but the ones I found, either solve only a single specific numerical example, or describe the general solution in a descriptive, hand-waving manner, i.e., without showing the specific equations and procedure.  So I'm trying to write code to automate this, but I'm not at all confident in the underlying math that I'm coding, because it's mostly my own synthesis of what I think I understand.  I give all this disclaimer, because so far I'm not convinced that the values I'm seeing are correct.

I found a very-sketchy C++ sample, which I used as a starting point.  I have very low confidence in this code, although I can't find a specific problem with it so far and it looks roughly plausible.  For one thing, almost all the variables were declared as "int", which seems impossible and erroneous.  I copied the code, but changed most of the variable types to "double".  And the C++ code used "pow(num, 2)" to square things.  Maybe there's some valid Computer Science reason to do that?  But to me, "(num * num)" is more to the point.  So I hope I didn't break the code through somehow misunderstanding it, but I think I fixed it from what had to be almost an intentionally-broken state.  Something about not giving ready-made answers to people on the Net, make sure they work a little and understand what they're using?  Anyway, inconvenient at the least...

https://www.geeksforgeeks.org/equation-of-circle-when-three-points-on-the-circle-are-given/

Here's the function I came up with.  But as I say, results don't look right to me, yet.  I may try writing a different function, directly from "first principles", so that I eliminate the (distinct) possibility that the original C++ code was totally nuts.

void
find_circle(double * cx, double * cy, double * r,
  double x1, double y1, double x2, double y2, double x3, double y3)
{
    double x12, x13, y12, y13, y31, y21, x31, x21, sx13, sy13, sx21, sy21;
    double f, g, h, k, c, sqr_of_r;

    x12 = x1 - x2;
    x13 = x1 - x3;
    y12 = y1 - y2;
    y13 = y1 - y3;
    y31 = y3 - y1;
    y21 = y2 - y1;
    x31 = x3 - x1;
    x21 = x2 - x1;
    /*  x1^2 - x3^2  */
    sx13 = (x1 * x1) - (x3 * x3);
    /*  y1^2 - y3^2  */
    sy13 = (y1 * y1) - (y3 * y3);
    sx21 = (x2 * x2) - (x1 * x1);
    sy21 = (y2 * y2) - (y1 * y1);
    f = ((sx13) * (x12)
      + (sy13) * (x12)
      + (sx21) * (x13)
      + (sy21) * (x13))
      / (2 * ((y31) * (x12) - (y21) * (x13)));
    g = ((sx13) * (y12)
      + (sy13) * (y12)
      + (sx21) * (y13)
      + (sy21) * (y13))
      / (2 * ((x31) * (y12) - (x21) * (y13)));
    c = -(x1 * x1) - (y1 * y1) - 2 * g * x1 - 2 * f * y1;
    /*  eqn of circle is x^2 + y^2 + 2*g*x + 2*f*y + c = 0
     *  where centre is (h = -g, k = -f) and radius r
     *  as r^2 = h^2 + k^2 - c  */
    h = -g;
    k = -f;
    sqr_of_r = h * h + k * k - c;
    *r = sqrt(sqr_of_r);
    *cx = h;
    *cy = k;
}

I should mention, the code above is based on what I might call the "Pythagorean" approach to circle-finding; and as I mentioned, I might rewrite from scratch, and if I do, I'll also be writing a "Pythagorean" approach.

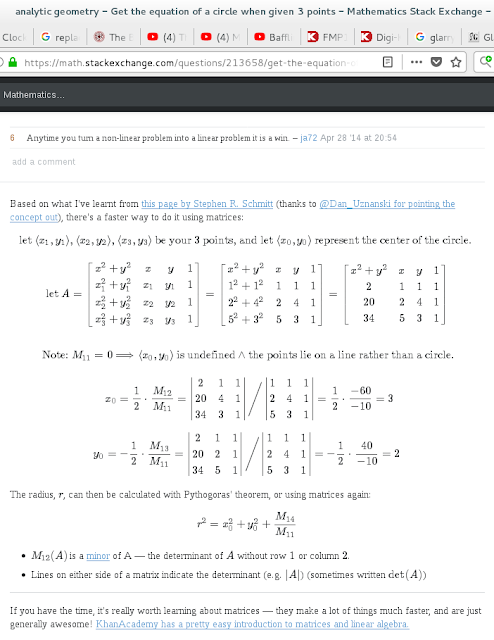
Another approach, which may be better in various ways, is the "matrix way".  Here's a screenshot which may guide you along this path, if interested: